雖然這篇numpy append速度鄉民發文沒有被收入到精華區:在numpy append速度這個話題中,我們另外找到其它相關的精選爆讚文章
在 numpy產品中有155篇Facebook貼文,粉絲數超過5萬的網紅軟體開發學習資訊分享,也在其Facebook貼文中提到, NT 390 特價中 開始你的機器學習和資料科學職涯,從數學、Python 和程式庫如:SKlearn、Pandas、NumPy、Matplotlib 和 Gym https://softnshare.com/complete-machine-learning-python-math-dummy...
同時也有202部Youtube影片,追蹤數超過12萬的網紅prasertcbs,也在其Youtube影片中提到,ดาวน์โหลด Jupyter Notebook ที่ใช้ในคลิปได้ที่ ► https://github.com/prasertcbs/scikitlearn_tutorial/blob/main/notebook/lightgbm_classifier_titanic.ipyn...
-
numpy 在 prasertcbs Youtube 的最佳解答
2021-05-02 11:00:07ดาวน์โหลด Jupyter Notebook ที่ใช้ในคลิปได้ที่ ► https://github.com/prasertcbs/scikitlearn_tutorial/blob/main/notebook/lightgbm_classifier_titanic.ipynb
เชิญสมัครเป็นสมาชิกของช่องนี้ได้ที่ ► https://www.youtube.com/subscription_center?add_user=prasertcbs
สอน Machine learning ► https://www.youtube.com/playlist?list=PLoTScYm9O0GH_3VrwwnQafwWQ6ibKnEtU
สอน Jupyter Notebook ► https://www.youtube.com/playlist?list=PLoTScYm9O0GErrygsfQtDtBT4CloRkiDx
สอน Python สำหรับ data science ► https://www.youtube.com/playlist?list=PLoTScYm9O0GFVfRk_MmZt0vQXNIi36LUz
สอน pandas ► https://www.youtube.com/playlist?list=PLoTScYm9O0GGsOHPCeufxCLt-uGU5Rsuj
สอน numpy ► https://www.youtube.com/playlist?list=PLoTScYm9O0GFNEpzsCBEnkUwgAwOu_PWw
สอน matplotlib ► https://www.youtube.com/playlist?list=PLoTScYm9O0GGRvUsTmO8MQUkIuM1thTCf
สอน seaborn ► https://www.youtube.com/playlist?list=PLoTScYm9O0GGC9QvLlrQGvMYatTjnOUwR
สอนภาษาไพธอน Python เบื้องต้น ► https://www.youtube.com/playlist?list=PLoTScYm9O0GH4YQs9t4tf2RIYolHt_YwW
สอนภาษาไพธอน Python OOP ► https://www.youtube.com/playlist?list=PLoTScYm9O0GEIZzlTKPUiOqkewkWmwadW
สอนการใช้งานโปรแกรม R: https://www.youtube.com/playlist?list=PLoTScYm9O0GGSiUGzdWbjxIkZqEO-O6qZ
สอนภาษา R เบื้องต้น ► https://www.youtube.com/playlist?list=PLoTScYm9O0GF6qjrRuZFSHdnBXD2KVIC
#prasertcbs_datascience #prasertcbs #prasertcbs_pandas #prasertcbs_sklearn -
numpy 在 prasertcbs Youtube 的精選貼文
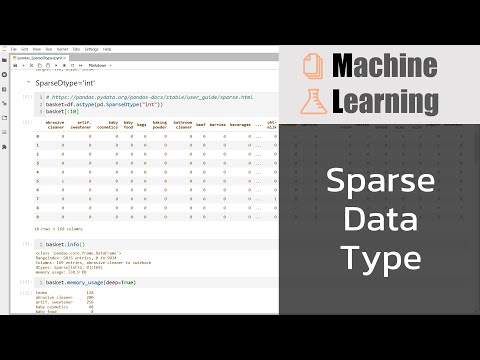
2021-04-27 22:13:34ดาวน์โหลด Jupyter Notebook ที่ใช้ในคลิปได้ที่ ► https://github.com/prasertcbs/scikitlearn_tutorial/blob/main/notebook/pandas_SparseDtype.ipynb
เชิญสมัครเป็นสมาชิกของช่องนี้ได้ที่ ► https://www.youtube.com/subscription_center?add_user=prasertcbs
สอน Machine learning ► https://www.youtube.com/playlist?list=PLoTScYm9O0GH_3VrwwnQafwWQ6ibKnEtU
สอน Jupyter Notebook ► https://www.youtube.com/playlist?list=PLoTScYm9O0GErrygsfQtDtBT4CloRkiDx
สอน Python สำหรับ data science ► https://www.youtube.com/playlist?list=PLoTScYm9O0GFVfRk_MmZt0vQXNIi36LUz
สอน pandas ► https://www.youtube.com/playlist?list=PLoTScYm9O0GGsOHPCeufxCLt-uGU5Rsuj
สอน numpy ► https://www.youtube.com/playlist?list=PLoTScYm9O0GFNEpzsCBEnkUwgAwOu_PWw
สอน matplotlib ► https://www.youtube.com/playlist?list=PLoTScYm9O0GGRvUsTmO8MQUkIuM1thTCf
สอน seaborn ► https://www.youtube.com/playlist?list=PLoTScYm9O0GGC9QvLlrQGvMYatTjnOUwR
สอนภาษาไพธอน Python เบื้องต้น ► https://www.youtube.com/playlist?list=PLoTScYm9O0GH4YQs9t4tf2RIYolHt_YwW
สอนภาษาไพธอน Python OOP ► https://www.youtube.com/playlist?list=PLoTScYm9O0GEIZzlTKPUiOqkewkWmwadW
สอนการใช้งานโปรแกรม R: https://www.youtube.com/playlist?list=PLoTScYm9O0GGSiUGzdWbjxIkZqEO-O6qZ
สอนภาษา R เบื้องต้น ► https://www.youtube.com/playlist?list=PLoTScYm9O0GF6qjrRuZFSHdnBXD2KVIC
#prasertcbs_datascience #prasertcbs #prasertcbs_pandas #prasertcbs_sklearn -
numpy 在 prasertcbs Youtube 的最佳貼文
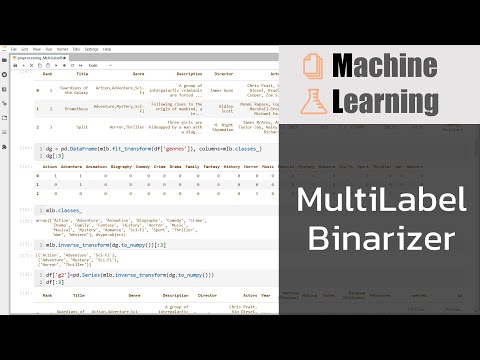
2021-04-25 22:15:47ดาวน์โหลด Jupyter Notebook ที่ใช้ในคลิปได้ที่ ► https://github.com/prasertcbs/scikitlearn_tutorial/blob/main/notebook/preprocessing_MultiLabelBinarizer.ipynb
เชิญสมัครเป็นสมาชิกของช่องนี้ได้ที่ ► https://www.youtube.com/subscription_center?add_user=prasertcbs
สอน Machine learning ► https://www.youtube.com/playlist?list=PLoTScYm9O0GH_3VrwwnQafwWQ6ibKnEtU
สอน Jupyter Notebook ► https://www.youtube.com/playlist?list=PLoTScYm9O0GErrygsfQtDtBT4CloRkiDx
สอน Python สำหรับ data science ► https://www.youtube.com/playlist?list=PLoTScYm9O0GFVfRk_MmZt0vQXNIi36LUz
สอน pandas ► https://www.youtube.com/playlist?list=PLoTScYm9O0GGsOHPCeufxCLt-uGU5Rsuj
สอน numpy ► https://www.youtube.com/playlist?list=PLoTScYm9O0GFNEpzsCBEnkUwgAwOu_PWw
สอน matplotlib ► https://www.youtube.com/playlist?list=PLoTScYm9O0GGRvUsTmO8MQUkIuM1thTCf
สอน seaborn ► https://www.youtube.com/playlist?list=PLoTScYm9O0GGC9QvLlrQGvMYatTjnOUwR
สอนภาษาไพธอน Python เบื้องต้น ► https://www.youtube.com/playlist?list=PLoTScYm9O0GH4YQs9t4tf2RIYolHt_YwW
สอนภาษาไพธอน Python OOP ► https://www.youtube.com/playlist?list=PLoTScYm9O0GEIZzlTKPUiOqkewkWmwadW
สอนการใช้งานโปรแกรม R: https://www.youtube.com/playlist?list=PLoTScYm9O0GGSiUGzdWbjxIkZqEO-O6qZ
สอนภาษา R เบื้องต้น ► https://www.youtube.com/playlist?list=PLoTScYm9O0GF6qjrRuZFSHdnBXD2KVIC
#prasertcbs_datascience #prasertcbs #prasertcbs_pandas #prasertcbs_sklearn


numpy 在 軟體開發學習資訊分享 Facebook 的最佳貼文
NT 390 特價中
開始你的機器學習和資料科學職涯,從數學、Python 和程式庫如:SKlearn、Pandas、NumPy、Matplotlib 和 Gym
https://softnshare.com/complete-machine-learning-python-math-dummy-to-pro/
numpy 在 軟體開發學習資訊分享 Facebook 的最佳貼文
NT 370 特價中
基本線性代數和微積分在 NumPy、TensorFlow 和 PyTorch 中的實戰應用
https://softnshare.com/machine-learning-data-science-foundations-masterclass/
numpy 在 軟體開發學習資訊分享 Facebook 的最佳解答
NT 390 特價中
建立 12 個以上的專案,學習 Web 開發、機器學習 + 更多
本課程的主題包括:
程式設計基礎
Python 基礎
Python 基本原理
資料結構
用 Python 做物件導向程式設計
Python 函數語言程式設計
Lambdas
Decorators
Generators
以 Python 進行測試
除錯
錯誤處理
正規表示式( Regular Expression )
Comprehensions
模組 ( Modules )
虛擬環境
開發環境(PyCharm,Jupyter 筆記本,VS Code,Sublime Text + 更多)
檔案處理: 影像,CSV,PDF,Text + 更多
用 Python 進行 Web 開發
利用 Python 進行機器學習
資料科學與 Python
使用 Python 和 Selenium 實現自動化
使用 Python 編寫指令碼( Scripting )
利用 Python 與 BeautifulSoup 進行 Web Scraping
影像檢測
資料視覺化
Kaggle,Pandas,NumPy,scikit-learn
用 Python 處理電郵及短訊
使用 API (Twitter Bot、密碼檢查器、翻譯器)
https://softnshare.com/complete-python-developer-zero-to-mastery/