雖然這篇function數學鄉民發文沒有被收入到精華區:在function數學這個話題中,我們另外找到其它相關的精選爆讚文章
在 function數學產品中有47篇Facebook貼文,粉絲數超過3,460的網紅Taipei Ethereum Meetup,也在其Facebook貼文中提到, 📜 [專欄新文章] ZKP 與智能合約的開發入門 ✍️ Johnson 📥 歡迎投稿: https://medium.com/taipei-ethereum-meetup #徵技術分享文 #使用心得 #教學文 #medium 這篇文章將以程式碼範例,說明 Zero Knowledge Proo...
同時也有1572部Youtube影片,追蹤數超過4萬的網紅吳老師教學部落格,也在其Youtube影片中提到,Python基礎程式語言應用證照班第10次上課 01_重點回顧與證照508最大公因數 02_證照508最大公因數解答 03_證照510費氏數列題目說明 04_證照510費氏數列無函式解答 05_證照510費氏數列加上函式解答 06_證照602撲克牌總和解答一 07_證照602撲克牌總和解答二改用串...
「function數學」的推薦目錄
- 關於function數學 在 就是Finance!投資趨勢 掌握主流 Instagram 的精選貼文
- 關於function數學 在 辣媽英文天后 林俐 Carol Instagram 的最佳解答
- 關於function數學 在 Herman Yeung Instagram 的最讚貼文
- 關於function數學 在 Taipei Ethereum Meetup Facebook 的精選貼文
- 關於function數學 在 史丹福狂想曲 Facebook 的精選貼文
- 關於function數學 在 吳老師excel函數與vba大數據教學 Facebook 的最讚貼文
- 關於function數學 在 吳老師教學部落格 Youtube 的最佳解答
- 關於function數學 在 吳老師教學部落格 Youtube 的最佳解答
- 關於function數學 在 吳老師教學部落格 Youtube 的精選貼文
function數學 在 就是Finance!投資趨勢 掌握主流 Instagram 的精選貼文
2021-08-02 14:35:57
[風險胃納risk appetite] 大部分的文字解釋皆於圖片中,因此以下文字只做為簡短輔助。 一切先從簡森不等式(Jensen’s inequality)談起,第二頁我們列出了簡森不等式的基本數學性質,在經濟及財務理論中,一般性的假設所有人皆為風險趨避者(risk averser),其對應的效...
function數學 在 辣媽英文天后 林俐 Carol Instagram 的最佳解答
2021-07-06 05:58:15
感謝大家這禮拜對吳迪老師、李傑老師直播秀的支持🙏🏻 俐媽明晚7:30~8:30也要開播了🎉🎉 俐媽要告訴大家上高中基本需要具備的心態、背英文單字的方法、還有學英文需要的一些工具(書/APP),歡迎三升一孩子參加! 大家一起一排愛心❤️刷起來! 今天送上之前預告的數學大餐part 2! (感謝學...
function數學 在 Herman Yeung Instagram 的最讚貼文
2021-02-02 10:20:03
各位同學大家好,有2件事想講 1. 我同牛牛出左一本中三數學的 e-book Herman Yeung F.3 Maths 中三數學 (Exercise 3C) (500題) 購買此 e-book (HK$199.00) 的連結︰ https://play.google.com/store/boo...
-
function數學 在 吳老師教學部落格 Youtube 的最佳解答
2021-09-14 22:35:23Python基礎程式語言應用證照班第10次上課
01_重點回顧與證照508最大公因數
02_證照508最大公因數解答
03_證照510費氏數列題目說明
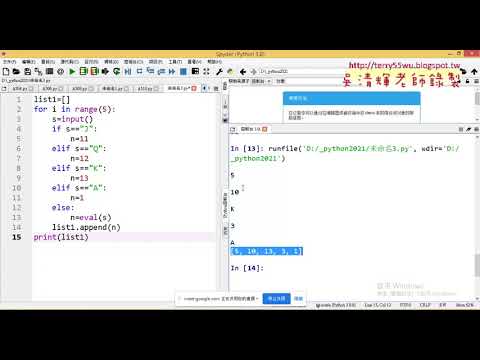
04_證照510費氏數列無函式解答
05_證照510費氏數列加上函式解答
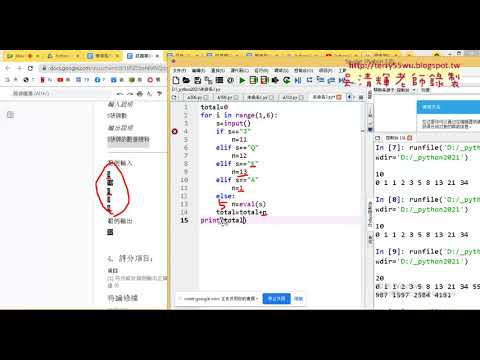
06_證照602撲克牌總和解答一
07_證照602撲克牌總和解答二改用串列
08_證照604眾數建立串列與新增
09_證照604眾數用COUNT計算次數
完整教學
http://goo.gl/aQTMFS
吳老師教學論壇
http://www.tqc.idv.tw/
教學論壇(之後課程會放論壇上課學員請自行加入):
https://groups.google.com/g/tcfst_python_2021_2
證照基礎程式語言 (Python 3)證照
Python 第1類:基本程式設計
技能內容:變數與常數、指定敘述、標準輸入輸出、運算式、算術運算子、數學函式的應用、格式化的輸出Python 第2類:選擇敘述
技能內容:if、if...else、if…elifPython 第3類:迴圈敘述
技能內容:while、for…inPython 第4類:進階控制流程
技能內容:常用的控制結構、條件判斷、迴圈Python 第5類:函式(Function)
技能內容:函式使用、傳遞參數、回傳資料、內建函式、區域變數與全域變數
上課用書:
Python 3.x 程式語言特訓教材(第二版)
作者: 蔡明志, 財團法人中華民國電腦技能基金會
出版社:全華
出版日期:2018/12/20
定價:490元
吳老師 110/9/14
EXCEL,VBA,Python,自強工業基金會,EXCEL,VBA,函數,程式設計,線上教學,PYTHON安裝環境 -
function數學 在 吳老師教學部落格 Youtube 的最佳解答
2021-09-14 22:34:53Python基礎程式語言應用證照班第10次上課
01_重點回顧與證照508最大公因數
02_證照508最大公因數解答
03_證照510費氏數列題目說明
04_證照510費氏數列無函式解答
05_證照510費氏數列加上函式解答
06_證照602撲克牌總和解答一
07_證照602撲克牌總和解答二改用串列
08_證照604眾數建立串列與新增
09_證照604眾數用COUNT計算次數
完整教學
http://goo.gl/aQTMFS
吳老師教學論壇
http://www.tqc.idv.tw/
教學論壇(之後課程會放論壇上課學員請自行加入):
https://groups.google.com/g/tcfst_python_2021_2
證照基礎程式語言 (Python 3)證照
Python 第1類:基本程式設計
技能內容:變數與常數、指定敘述、標準輸入輸出、運算式、算術運算子、數學函式的應用、格式化的輸出Python 第2類:選擇敘述
技能內容:if、if...else、if…elifPython 第3類:迴圈敘述
技能內容:while、for…inPython 第4類:進階控制流程
技能內容:常用的控制結構、條件判斷、迴圈Python 第5類:函式(Function)
技能內容:函式使用、傳遞參數、回傳資料、內建函式、區域變數與全域變數
上課用書:
Python 3.x 程式語言特訓教材(第二版)
作者: 蔡明志, 財團法人中華民國電腦技能基金會
出版社:全華
出版日期:2018/12/20
定價:490元
吳老師 110/9/14
EXCEL,VBA,Python,自強工業基金會,EXCEL,VBA,函數,程式設計,線上教學,PYTHON安裝環境 -
function數學 在 吳老師教學部落格 Youtube 的精選貼文
2021-09-14 22:34:37Python基礎程式語言應用證照班第10次上課
01_重點回顧與證照508最大公因數
02_證照508最大公因數解答
03_證照510費氏數列題目說明
04_證照510費氏數列無函式解答
05_證照510費氏數列加上函式解答
06_證照602撲克牌總和解答一
07_證照602撲克牌總和解答二改用串列
08_證照604眾數建立串列與新增
09_證照604眾數用COUNT計算次數
完整教學
http://goo.gl/aQTMFS
吳老師教學論壇
http://www.tqc.idv.tw/
教學論壇(之後課程會放論壇上課學員請自行加入):
https://groups.google.com/g/tcfst_python_2021_2
證照基礎程式語言 (Python 3)證照
Python 第1類:基本程式設計
技能內容:變數與常數、指定敘述、標準輸入輸出、運算式、算術運算子、數學函式的應用、格式化的輸出Python 第2類:選擇敘述
技能內容:if、if...else、if…elifPython 第3類:迴圈敘述
技能內容:while、for…inPython 第4類:進階控制流程
技能內容:常用的控制結構、條件判斷、迴圈Python 第5類:函式(Function)
技能內容:函式使用、傳遞參數、回傳資料、內建函式、區域變數與全域變數
上課用書:
Python 3.x 程式語言特訓教材(第二版)
作者: 蔡明志, 財團法人中華民國電腦技能基金會
出版社:全華
出版日期:2018/12/20
定價:490元
吳老師 110/9/14
EXCEL,VBA,Python,自強工業基金會,EXCEL,VBA,函數,程式設計,線上教學,PYTHON安裝環境



function數學 在 Taipei Ethereum Meetup Facebook 的精選貼文
📜 [專欄新文章] ZKP 與智能合約的開發入門
✍️ Johnson
📥 歡迎投稿: https://medium.com/taipei-ethereum-meetup #徵技術分享文 #使用心得 #教學文 #medium
這篇文章將以程式碼範例,說明 Zero Knowledge Proofs 與智能合約的結合,能夠為以太坊的生態系帶來什麼創新的應用。
本文為 Tornado Cash 研究系列的 Part 2,本系列以 tornado-core 為教材,學習開發 ZKP 的應用,另兩篇為:
Part 1:Merkle Tree in JavaScript
Part 3:Tornado Cash 實例解析
Special thanks to C.C. Liang for review and enlightenment.
近十年來最強大的密碼學科技可能就是零知識證明,或稱 zk-SNARKs (zero knowledge succinct arguments of knowledge)。
zk-SNARKs 可以將某個能得出特定結果 (output) 的計算過程 (computation),產出一個證明,而儘管計算過程可能非常耗時,這個證明卻可以快速的被驗證。
此外,零知識證明的額外特色是:你可以在不告訴對方輸入值 (input) 的情況下,證明你確實經過了某個計算過程並得到了結果。
上述來自 Vitalik’s An approximate introduction to how zk-SNARKs are possible 文章的首段,該文說是給具有 “medium level” 數學程度的人解釋 zk-SNARKs 的運作原理。(可惜我還是看不懂 QQ)
本文則是從零知識證明 (ZKP) 應用開發的角度,結合電路 (circuit) 與智能合約的程式碼來說明 ZKP 可以為既有的以太坊智能合約帶來什麼創新的突破。
基本上可以謹記兩點 ZKP 帶來的效果:
1. 擴容:鏈下計算的功能。
2. 隱私:隱藏秘密的功能。
WithoutZK.sol
首先,讓我們先來看一段沒有任何 ZKP 的智能合約:
這份合約的主軸在 process(),我們向它輸入一個秘密值 secret,經過一段計算過程後會與 answer 比對,如果驗證成功就會改寫變數 greeting 為 “answer to the ultimate question of life, the universe, and everything”。
Computation
而計算過程是一個簡單的函式:f(x) = x**2 + 6。
我們可以輕易推出秘密就是 42。
這個計算過程有很多可能的輸入值 (input) 與輸出值 (output):
f(2) = 10
f(3) = 15
f(4) = 22
…
但是能通過驗證的只有當輸出值和我們存放在合約的資料 answer 一樣時,才會驗證成功,並執行 process 的動作。
可以看到有一個 calculate 函式,說明這份合約在鏈上進行的計算,以及 process 需要輸入參數 _secret,而我們知道合約上所有交易都是公開的,所以這個 _secret 可以輕易在 etherscan 上被看到。
從這個簡單的合約中我們看到 ZKP 可以解決的兩個痛點:鏈下計算與隱藏秘密。
Circuits
接下來我們就改寫這份合約,加入 ZKP 的電路語言 circom,使用者就能用他的 secret 在鏈下進行計算後產生一個 proof,這 proof 就不會揭露有關 secret 的資訊,同時證明了當 secret 丟入 f(x) = x**2 + 6 的計算過程後會得出 1770 的結果 (output),把這個 proof 丟入 process 的參數中,經過 Verifier 的驗證即可執行 process 的內容。
有關電路 circuits 的環境配置,可以參考 ZKP Hello World,這裡我們就先跳過去,直接來看 circom 的程式碼:
template Square() { signal input in; signal output out; out <== in * in;}template Add() { signal input in; signal output out; out <== in + 6;}template Calculator() { signal private input secret; signal output out; component square = Square(); component add = Add(); square.in <== secret; add.in <== square.out; out <== add.out;}component main = Calculator();
這段就是 f(x) = x**2 + 6 在 circom 上的寫法,可能需要時間去感受一下。
ZK.sol
circom 寫好後,可以產生一個 Verifier.sol 的合約,這個合約會有一個函式 verifyProof,於是我們把上方的合約改寫成使用 ZKP 的樣子:
我們可以發現 ZK 合約少了 calculate 函式,顯然 f(x) = x**2 + 6 已經被我們寫到電路上了。
snarkjs
產生證明的程式碼以 javascript 寫成如下:
let { proof, publicSignals } = await groth16.fullProve(input, wasmPath, zkeyPath);
於是提交 proof 給合約,完成驗證,達到所謂鏈下計算的功能。
最後讓我們完整看一段 javascript 的單元測試,使用 snarkjs 來產生證明,對合約的 process 進行測試:
對合約來說, secret = 42 是完全不知情的,因此隱藏了秘密。
publicSignals
之前不太清楚 publicSignals 的用意,因此在這裡特別說明一下。
基本上在產生證明的同時,也會隨帶產生這個 circom 所有的 public 值,也就是 publicSignals,如下:
let { proof, publicSignals } = await groth16.fullProve(input, wasmPath, zkeyPath);
在我們的例子中 publicSignals 只有一個,就是 1770。
而 verifyProof 要輸入的參數除了 proof 之外,也要填入 public 值,簡單來說會是:
const isValid = verifyProof(proof, publicSignals);
問題來了,我們在設計應用邏輯時,當使用者要提交參數進行驗證的時候,publicSignals 會是由「使用者」填入嗎?或者是說,儘管是使用者填入,那它需不需要先經過檢查,才可以填入 verifyProof?
關鍵在於我們的合約上存有一筆資料:answer = 1770
回頭看合約上的 process 在進行 verifyProof 之前,必須要檢查 isAnswer(publicSignals[0]):
想想要是沒有檢查 isAnswer,這份合約會發生什麼事情?
我們的應用邏輯就會變得毫無意義,因為少了要驗證的答案,就只是完成計算 f(42) = 1770,那麼不論是 f(1) = 7 或 f(2) = 10,使用者都可以自己產生證明與結果,自己把 proof 和 publicSignals 填入 verifyProof 的參數中,都會通過驗證。
至此可以看出,ZKP 只有把「計算過程」抽離到鏈下的電路,計算後的結果仍需要與鏈上既有的資料進行比對與確認後,才能算是有效的應用 ZKP。
應用邏輯的開發
本文主要談到的是 zk-SNARKs 上層應用邏輯的開發,關於 ZKP 的底層邏輯如上述使用的 groth16 或其他如 plonk 是本文打算忽略掉的部分。
從上述的例子可以看到,即使我們努力用 circom 實作藏住 secret,但由於計算過程太過簡單,只有 f(x) = x**2+6,輕易就能從 answer 反推出我們的 secret 是 42,因此在應用邏輯的開發上,也必須注意 circom 的設計可能出了問題,導致私密訊息容易外洩,那儘管使用再強的 ZKP 底層邏輯,在應用邏輯上有漏洞,也沒辦法達到隱藏秘密的效果。
此外,在看 circom 的程式碼時,可以關注最後一個 template 的 private 與 public 值分別是什麼。以本文的 Calculator 為例,private 值有 secret,public 值有 out。
另外補充:
如果有個 signal input 但它不是 private input,就會被歸類為 public。
一個 circuit 至少會有一個 public,因為計算過程一定會有一個結果。
最後,在開發的過程中我會用 javascript 先實作計算過程,也可以順便產出 input.json,然後再用 circom 語言把計算過程實現,產生 proof 和 public 後,再去對照所有 public 值和 private 值,確認是不是符合電路計算後所要的結果,也就是比較 javascript 算出來的和 circom 算出來的一不一樣,如果不一樣就能確定程式碼是有 bug 的。
參考範例:https://github.com/chnejohnson/circom-playground
總結
本文的程式碼展現 ZKP 可以做到鏈下計算與隱藏秘密的功能,在真實專案中,可想而知電路的計算過程不會這麼單純。
會出現在真實專案中的計算像是 hash function,複雜一點會加入 Merkle Tree,或是電子簽章 EdDSA,於是就能產生更完整的應用如 Layer 2 擴容方案之一的 ZK Rollup,或是做到匿名交易的 Tornado Cash。
本文原始碼:https://github.com/chnejohnson/mini-zkp
下篇文章就來分享 Tornado Cash 是如何利用 ZKP 達成匿名交易的!
參考資料
概念介紹
Cryptography Playground
zk-SNARKs-Explainer
神奇的零知識證明!既能保守秘密,又讓別人信你!
認識零知識證明 — COSCUP 2019 | Youtube
應用零知識證明 — COSCUP 2020 | Youtube
ZK Rollup
動手實做零知識 — circom — Kimi
ZK-Rollup 开发经验分享 Part I — Fluidex
ZkRollup Tutorial
ZK Rollup & Optimistic Rollup — Kimi Wu | Medium
Circom
circom/TUTORIAL.md at master · iden3/circom · GitHub
ZKP Hello World
其他
深入瞭解 zk-SNARKs
瞭解神秘的 ZK-STARKs
zk-SNARKs和zk-STARKs解釋 | Binance Academy
[ZKP 讀書會] MACI
Semaphore
Zero-knowledge Virtual Machines, the Polaris License, and Vendor Lock-in | by Koh Wei Jie
Introduction & Evolution of ZK Ecosystem — YouTube
The Limitations of Privacy — Barry Whitehat — YouTube
Introduction to Zero Knowledge Proofs — Elena Nadolinski
ZKP 與智能合約的開發入門 was originally published in Taipei Ethereum Meetup on Medium, where people are continuing the conversation by highlighting and responding to this story.
👏 歡迎轉載分享鼓掌
function數學 在 史丹福狂想曲 Facebook 的精選貼文
相信各位朋友都知道,史丹福除了喜歡血液學外,亦對數學非常有興趣。最近有朋友給我看了一篇有趣的文章,文章刊登在《Bulletin of Mathematical Biology》期刊中。文章的作者為裂口型紅細胞(stomatocytes)與鋸齒狀紅血球(echinocytes)兩種異常的紅血球建立了數學模型,嘗試讓我們更了解它們的結構。當中更涉及到雅可比橢圓函數(Jacobi elliptical function)等高等數學,非常有趣。
裂口型紅細胞是中央有裂縫的紅血球,頗像張開的口。它們可以在先天性裂口型紅細胞增多症(hereditary stomatocytosis)或東南亞卵圓形紅細胞增多症(Southeast Asian ovalocytosis)的病人中找到。至於鋸齒狀紅血球則外圍有如針狀的凸起,凸起的程度小且多,並在細胞膜上均勻分布。這種細胞常在腎功能衰退的病人中出現,但有時候則純粹是抽血瓶使用EDTA抗凝血劑引起的現象,可以在完全正常的血液中出現。
利用數學方法來研究紅血球形狀這方法非常新穎有趣,也不禁令我想起讀大學時期的老師黎青龍教授的名言--No knowledge is useless。數學看似抽象且「離地」,與日常生活相距遙遠,有人甚至覺得數學是「沒有用」的學問。但其實只要用得其所,數學的應用空間其實很大,就連紅血球形狀這樣的問題都有用得到數學的地方。
有興趣的朋友可參考以下文章:
https://www.researchgate.net/publication/221710602_Mathematical_models_of_naturally_morphed_human_erythrocytes_stomatocytes_and_echinocytes
function數學 在 吳老師excel函數與vba大數據教學 Facebook 的最讚貼文
從EXCEL高階函數到VBA程式設計工作坊(師大)
01_手機範例利用TEXT與VALUE與樞紐分析表與圖
02_開啟開發人員與錄製巨集與增加按鈕
03_範例151括弧字串用FIND與MID與IFERROR
04_北市住宅竊盜點位公式MID與FIND與IFERROR函數
完整影音
https://www.youtube.com/playlist?list=PLgzs-Q3byiYMAO45ZAemuL9p3Hxhi2EBp
課程目標
提高工作效率:自然不用加班、工作更愜意
培養VBA程式專業技能:增加職場升遷或轉職籌碼
課程目標:
1.熟悉EXCEL內建各類別250幾個函數(理解代替死背)
2.從函數到VBA設計(Sub)與自訂函數(Function)
3.錄製巨集與編修VBA程式
4.學會VBA的重要使用技巧(變數、迴圈與邏輯)
5.學會VBA表單設計與將EXCEL當資料庫
6.學會快速下載網頁資料(巨集錄製、迴圈、邏輯)
進階班
7.用EXCEL做銷貨單與查詢系統
8.資料庫、多工作表、工作簿、網路爬蟲等應用
?9.EXCEL VBA與樞紐分析表視覺化報表
10. EXCEL VBA與Python程式協同應用
五大類函數與自訂函數
一、文字和資料函數
二、邏輯函數
三、日期和時間函數
四、數學和三角函數
五、檢視和參照函數
上課用書:
Excel VBA一點都不難:一鍵搞定所有報表
作者: Excel Home
出版社:博碩
出版日期:2013/06/26
定價:380元
超圖解 Excel VBA 基礎講座
作者: 亮亨/譯 出版社:旗標
出版日期:2006/05/15 定價:420元
日本Amazon網站同類書籍銷售No.1
吳老師 110/4/21
台灣師範大學,運算思維融入教學,函數,程式設計,線上教學excel vba教學電子書,excel vba範例,vba語法,vba教學網站,vba教學講義,vba範例教學,excel vba教學視頻